British museum
The British Museum algorithm is a general approach to find a solution by checking all possibilities one by one, beginning with the smallest. The term refers to a conceptual, not a practical, technique where the number of possibilities is enormous.
For example, this can be archived by generating a set of random paths, and check every single path if it fulfills the requirement. In this exercise we will take a look at a “British museum”, where we will try to find a path from starting point, to our final point in 2D grid word.
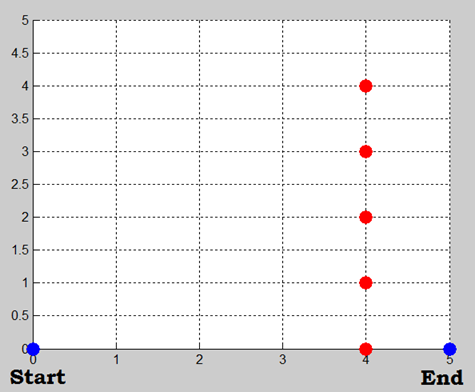
Grid word with start finish and red obstacles
Note.: British museum is not actually named after the route in the British museum, but it was derived from an infinite monkey problem, “… since it seemed to them as sensible as placing monkeys in front of typewriters in order to reproduce all the books in the British Museum.”
The algorithm that we use will be slightly modified, and goes as followed:
- Take a look at actual position, and decide if the position can be expanded (if we can move to any neighboring place.
- If you can expand the node, then do so, and add the expanded node as the actual position. Also store the expanded node with its node index (preferably index in final path from the start)
- If node cannot be expanded, then take a look in previous node (from the stored path), and set previous node as actual node)
- Repeat process until the actual position is equal to the finish position
Before expanding the node, it is worth checking if the node is in grid N ∈ <0-board size>. Also, you should check if its not a obstacle (red dot in grid), or if it was not previously expanded. This fill limit the infinity loop of some nodes.
To make it more „obvious “, it is recommended to not use fixed set of expansions (i.e.: left – right – top – bottom), but use a random expansion indexing.
| Data | Value |
|---|---|
| Theory | https://en.wikipedia.org/wiki/British_Museum_algorithm |
| Code | Brit_muzeum_code.zip |
| Solution code | Brit_muzeum_solution_code.zip |